Confirmatory factor analysis of a rubric for assessing algorithmic thinking on undergraduate students
Análisis factorial confirmatorio de una rúbrica para evaluar pensamiento algorítmico en estudiantes universitarios
Análise fatorial confirmatória de uma rubrica para avaliar o pensamento algorítmico em estudantes universitários
DOI: https://doi.org/10.18861/cied.2024.15.2.3797
Eduardo
Adam Navas-López
Universidad de El Salvador
El
Salvador
eduardo.navas@ues.edu.sv
ORCID:
0000-0003-3684-2966
Received:
March 27, 24
Approved:
July 1, 24
How
to cite:
Navas-López,
E. A. (2024). Confirmatory factor analysis of a rubric for assessing
algorithmic thinking on undergraduate students. Cuadernos
de Investigación Educativa,
15(2).
https://doi.org/10.18861/cied.2024.15.2.3797
Abstract
Algorithmic thinking is a key element for individuals to be aligned with the computer era. Its study is important not only in the context of computer science but also in mathematics education and all STEAM contexts. However, despite its importance, a lack of research treating it as an independent construct and validating its operational definitions or rubrics to assess its development in university students through confirmatory factor analysis has been discovered. The aim of this paper is to conduct a construct validation through confirmatory factor analysis of a rubric for the algorithmic thinking construct, specifically to measure its level of development in university students. Confirmatory factor analysis is performed on a series of models based on an operational definition and a rubric previously presented in the literature. The psychometric properties of these models are evaluated, with most of them being discarded. Further research is still needed to expand and consolidate a useful operational definition and the corresponding rubric to assess algorithmic thinking in university students. However, the confirmatory factor analysis confirms the construct validity of the rubric, as it exhibits very good psychometric properties and leads to an operational definition of algorithmic thinking composed of four components: Problem analysis, algorithm construction, input case identification, and algorithm representation.
Keywords: algorithmic thinking, higher education students, educational assessment, confirmatory factor analysis, STEM education.
Resumen
El pensamiento algorítmico es un elemento clave para ser un individuo alineado con la era de la computación. Su estudio es importante no solo en el contexto de las ciencias de la computación, sino también en la didáctica de la matemática y en todos los contextos STEAM. Pero a pesar de su importancia, se ha descubierto una carencia de investigaciones que lo traten como un constructo independiente y que validen sus definiciones operacionales o rúbricas para evaluar su desarrollo en estudiantes universitarios mediante análisis factorial confirmatorio. El objetivo de este artículo es realizar una validación de constructo por medio de análisis factorial confirmatorio de una rúbrica para el constructo pensamiento algorítmico, específicamente para medir su nivel de desarrollo en estudiantes universitarios. Se realiza un análisis factorial confirmatorio sobre una serie de modelos basados en una definición operacional y una rúbrica previamente presentadas en la literatura. Se evalúan las propiedades psicométricas de estos modelos, descartándose la mayoría de ellos. Aún se necesita más investigación para ampliar y consolidar una definición operacional útil, y la rúbrica correspondiente, para evaluar el pensamiento algorítmico en estudiantes universitarios. Sin embargo, el análisis factorial confirmatorio llevado a cabo confirma la validez de constructo de la rúbrica, ya que presenta muy buenas propiedades psicométricas y conduce a una definición operacional de pensamiento algorítmico compuesta por cuatro componentes: análisis del problema, construcción del algoritmo, identificación de los casos de entrada y representación del algoritmo.
Palabras clave: pensamiento algorítmico, estudiantes de educación superior, evaluación educativa, análisis factorial confirmatorio, educación STEM.
Resumo
O pensamento algorítmico é um elemento-chave para que os indivíduos estejam alinhados com a era da computação. Seu estudo é importante não apenas no âmbito da ciência da computação, mas também na didática da matemática e em todos os contextos STEAM. No entanto, apesar de sua importância, faltam pesquisas que o tratem como um construto independente e que validem suas definições operacionais ou rubricas para avaliar seu desenvolvimento em estudantes universitários por meio de análises fatoriais confirmatórias. O objetivo deste artigo é realizar uma validação de construto por meio de análise fatorial confirmatória de uma rubrica para o construto pensamento algorítmico, especificamente para medir seu nível de desenvolvimento em estudantes universitários. É realizada uma análise fatorial confirmatória sobre uma série de modelos baseados em uma definição operacional e uma rubrica previamente apresentadas na literatura. As propriedades psicométricas desses modelos são avaliadas, e a maioria deles é descartada. Ainda são necessárias mais pesquisas para ampliar e consolidar uma definição operacional útil e a rubrica correspondente para avaliar o pensamento algorítmico em estudantes universitários. No entanto, a análise fatorial confirmatória realizada confirma a validade de construto da rubrica, pois esta apresenta propriedades psicométricas muito boas, e conduz a uma definição operacional de pensamento algorítmico composta por quatro componentes: análise do problema, construção do algoritmo, identificação dos casos de entrada, e representação do algoritmo.
Palavras-chave: pensamento algorítmico, estudantes do ensino superior, avaliação educacional, análise fatorial confirmatória, educação STEAM.
Introduction
Computational thinking (CT) is becoming a fundamental skill for 21st-century citizens worldwide (Grover & Pea, 2018; Nordby et al., 2022) since it is related to beneficial skills that are considered applicable in everyday life (Wing, 2006; 2017). Algorithmic thinking (AT) is considered the main component of CT (Juškevičienė, 2020; Selby & Woollard, 2013; Stephens & Kadijevich, 2020). Moreover, most of the CT definitions have their roots in AT (Juškevičienė, 2020), although some very influential CT definitions do not mention AT at all (Shute et al., 2017; Weintrop et al., 2016; Wing, 2006).
Today, daily life is surrounded by algorithms and governed by algorithms, so AT is considered one of the key elements to be an individual aligned with the era of computing (Juškevičienė, 2020). Research on AT is very important in computer science education, but it also has a vital role in mathematics education and STEAM contexts (Kadijevich et al., 2023). Despite its importance, AT has been found to lack research that treats it as an independent construct with independent-of-CT assessments (Park & Jun, 2023).
CT is still a blurry psychological construct, and its assessment remains a thorny, unresolved issue (Bubica & Boljat, 2021; Martins-Pacheco et al., 2020; Román-González et al., 2019; Tang et al., 2020), and open, as a research challenge, demanding scholars’ attention urgently (Poulakis & Politis, 2021). Moreover, the same happens with AT (Lafuente Martínez et al., 2022; Stephens & Kadijevich, 2020) due to its relationship with CT.
A wide variety of CT assessment tools are available (Tang et al., 2020; Zúñiga Muñoz et al., 2023), ranging from diagnostic tools to measures of CT proficiency and assessments of perceptions and attitudes towards this thinking way, among others. (Román-González et al., 2019). However, empirical research evaluating the validity and reliability of these instruments remains relatively low compared to the volume of research in this area (Tang et al., 2020). Consequently, as noted by Bubica and Boljat (2021), “there is still not enough research on CT evaluation to provide teachers with enough support in the field” (p. 453).
While much research focuses on measuring and assessing CT (Poulakis & Politis, 2021), the same cannot be said for AT. Moreover, these research streams do not converge (Stephens & Kadijevich, 2020). Furthermore, a limited percentage of research on CT assessment is directed towards undergraduate students (Tang et al., 2020).
A limited number of efforts, albeit divergent, have been made to formulate operational definitions for AT, as evidenced by works such as those by Juškevičienė and Dagienė (2018), Lafuente Martínez et al. (2022), Navas-López (2021), and Park and Jun (2023). Additionally, attempts have been undertaken to develop an assessment rubric (Navas-López, 2021) and apply confirmatory factor analysis (CFA) for AT measurement instruments (Bubica & Boljat, 2021; Lafuente Martínez et al., 2022).
Despite these contributions, there remains a notable gap in the literature regarding validating instruments specifically designed to assess AT as an independent construct distinct from CT. So far, there are only two factorial models for AT in adolescents or adults with acceptable psychometric properties: a unifactorial model (Lafuente Martínez et al., 2022) and a bifactorial model (Ortega Ruipérez et al., 2021). Therefore, this research endeavors to develop a more detailed factorial model through the construct validation of the rubrics applied by Navas-López (2021) to assess AT in undergraduate students.
Developing reliable instruments for studying AT is crucial, particularly with the rising integration of CT and AT in basic education curricula around the world (Kadijevich et al., 2023). Continuous research is crucial to identify components, dimensions, and factors that illuminate the assessment of AT (Lafuente Martínez et al., 2022; Park & Jun, 2023).
Literature
review
Some
definitions
As this paper focuses on AT, it is crucial to understand the concept of an algorithm clearly. According to Knuth (1974), an algorithm is defined as "a precisely-defined sequence of rules instructing how to generate specified output information from given input information within a finite number of steps" (p. 323). This definition encompasses human and machine execution without specifying any particular technology requirement.
In line with this definition, Lockwood et al. (2016) describe AT as “a logical, organized way of thinking used to break down a complicated goal into a series of (ordered) steps using available tools” (p. 1591). This definition of AT, like the previous definition of algorithm, does not require the intervention of any specific technology.
For Futschek (2006), AT is the following set of skills that are connected to the construction and understanding of algorithms:
a. the ability to analyze given problems,
b. the ability to specify a problem precisely,
c. the ability to find the basic actions that are adequate to the given problem,
d. the ability to construct a correct algorithm for a given problem using the basic actions,
e. the ability to think about all possible special and regular cases of a problem,
f. the ability to improve the efficiency of an algorithm. (p. 160)
There are other operational definitions for AT. Some of them emphasize specific skills, such as the correct implementation of branching and iteration structures (Grover, 2017; Bubica & Boljat, 2021). Most of them describe AT in terms of a list of skills (Bubica & Boljat, 2021; Lafuente Martínez et al., 2022; Lehmann, 2023; Park & Jun, 2023; Stephens & Kadijevich, 2020), such as analyzing algorithms or creating sequences of steps. Despite similarities, these skill lists cannot be considered equivalent to each other.
The definition of CT will now be addressed by expanding on the concept of AT. It could be defined as “the thought processes involved in formulating a problem and expressing its solution(s) in such a way that a computer –human or machine– can effectively carry out” (Wing, 2017, p. 8). Unlike the AT definitions, this CT definition allows for machines' involvement. Consequently, CT does involve considerations about the technology underlying the execution of these solutions (Navas-López, 2024).
As with AT, different operational definitions of CT describe it as a list of various components or skills, such as abstraction, decomposition, and generalization (Otero Avila et al., 2019; Tsai et al., 2022). Additionally, several authors explicitly include AT as an operational component of CT in their empirical research (Bubica & Boljat, 2021; Korkmaz et al., 2017; Lafuente Martínez et al., 2022; Otero Avila et al., 2019; Tsai et al., 2022).
For Stephens and Kadijevich (2020), the cornerstones of AT are decomposition, abstraction, and algorithmization, whereas CT incorporates these elements along with automation. This distinction underscores that automation is the defining factor separating AT from CT.
Lehmann (2023) describes algorithmization as the ability to design a set of ordered steps to produce a solution or achieve a goal. These steps include inputs and outputs, basic actions, or algorithmic concepts such as iterations, loops, and variables. Note the similarity with Lockwood et al. (2016) definition of AT.
Kadijevich et al. (2023) assert that AT requires distinct cognitive skills, including abstraction and decomposition. Following Juškevičienė and Dagienė (2018), decomposition involves breaking down a problem into parts (sub-problems) that are easier to manage, while abstraction entails identifying essential elements of a problem or process, which involves suppressing details and making general statements summarizing particular examples. Furthermore, these two skills are present in many CT operational definitions (Bubica & Boljat, 2021; Juškevičienė & Dagienė, 2018; Lafuente Martínez et al., 2022; Martins-Pacheco et al., 2020; Otero Avila et al., 2019; Selby & Woollard, 2013; Shute et al., 2017).
Unsurprisingly, the most commonly assessed CT components are algorithms, abstraction, and decomposition (Martins-Pacheco et al., 2020), which closely aligns with the AT conception by Stephens and Kadijevich (2020). In fact, in the study conducted by Lafuente Martínez et al. (2022), the researchers aimed to validate a test for assessing CT in adults, avoiding technology (or automation). However, their CFA results suggest a simpler CT concept, governed by a single ability associated with recognizing and expressing routines to address problems or tasks, akin to systematic, step-by-step instructions—essentially, AT.
The distinction between AT and CT remains to be clarified in current scientific literature. Nonetheless, this study adopts Stephens and Kadijevich's (2020) perspective, emphasizing that the primary difference lies in automation. Specifically, AT excludes broader aspects of technology use and social implications (Navas-López, 2024). The study also focuses on abstraction and decomposition as integral components of AT.
Algorithmic
thinking and Computational thinking assessments
According to Bubica and Boljat (2021), “to evaluate CT, it is necessary to find evidence of a deeper understanding of a CT-relevant problem solved by a pupil, that is, to find evidence of understanding how the pupil created their coded solution” (p. 428). Grover (2017) recommends the use of open-ended questions for making “systems of assessments” to assess AT.
Bacelo and Gómez-Chacón (2023) emphasize the significance of unplugged activities for observing students' skills and behaviors, and identifying patterns that can reveal strengths and weaknesses in AT learning, as shown by Lehmann (2023). Empirical data suggests that students engaged in unplugged activities demonstrate marked improvements in CT skills compared to those in plugged activities (Kirçali & Özdener, 2023). Unplugged activities are generally effective in fostering CT skills (Chen et al., 2023), making them essential components in AT assessment instruments to identify patterns that reveal strengths and weaknesses.
There is a common tendency to assess AT and CT through small problem-solving tasks, often using binary criteria like 'solved/unsolved' or 'correct/incorrect' without detailed rubrics for each problem. Examples can be found across different age groups: young children (Kanaki & Kalogiannakis, 2022), K-12 education (Oomori et al., 2019; Ortega et al., 2021), and adults (Lafuente Martínez et al., 2022). Conversely, there are proposals to qualitatively assess CT using unplugged complex problems, focusing on students' cognitive processes (Lehmann, 2023).
In addition, Bubica and Boljat (2021) suggest adapting problem difficulty to students' level, because assessments for AT and CT vary in effectiveness for different learners (Grover, 2017). Therefore, an effective AT assessment should include unplugged, preferably open-ended problems adjusted to students' expected levels to identify cognitive processes better.
Validity
of CT/AT instruments through factor analysis
According to Lafuente Martínez et al. (2022), assessments designed to measure CT in adults, as discussed in the literature, often lack substantiated evidence concerning crucial validity aspects, particularly the internal structure and test content. Some studies validate CT instruments, which include the AT construct, through factor analysis, but they have problems with psychometric properties, such as those of Ortega Ruipérez and Asensio Brouard (2021), Bubica and Boljat (2021) and Sung (2022).
Ortega Ruipérez and Asensio Brouard (2021) shift the focus of CT assessment towards problem-solving to measure the performance of cognitive processes, moving away from computer programming and software design. Their research aims to validate an instrument for assessing CT through problem-solving in students aged 14-16 using CFA. However, the instrument exhibits low factor loadings, including one negative. By emphasizing problem-solving outside the realm of computer programming, this instrument aligns more closely with the interpretation of AT by Stephens and Kadijevich (2020), as it removes automation from CT. Nevertheless, its results are pretty poor, as the conducted CFA only identifies two independent factors: problem representation and problem-solving.
Bubica and Boljat (2021) applied an exploratory factor analysis for a CT instrument, special for the Croatian basic education curriculum, with a mix of simple answer questions and open-ended problems in students aged 11-12. AT evaluation criteria focus on sequencing, conditionals, and cycles. However, the factor loadings are low, and the grouping of the tasks (items) according to the factor analysis is strangely overloaded towards one factor.
Sung (2022) conducted a validation through CFA for two measurements to assess CT in young children aged 5 and 6 years. It has certain limitations, including the weak factor loadings of specific items, suboptimal internal consistency in subfactors, and low internal reliability. Furthermore, Sung (2022) reflects that “young children who are still cognitively developing and lack specific high-level thinking skills seem to be at a stage before CT’s major higher-order thinking functions are subdivided” (p. 12992). This may be the same problem in Bubica and Boljat’s (2021) study results.
Lafuente Martínez et al. (2022) performed a CFA for a CT instrument for adults (average 23.58 years), and they did not find multidimensionality in their evidence, thus failing to confirm the assumption of difference between CT and AT.
Other CFA studies focus on CT instruments with strong psychometric properties, but they primarily assess disposition toward CT rather than problem-solving abilities. For instance, Tsai et al. (2022) used CFA to validate their 19-item questionnaire, demonstrating good item reliability, internal consistency, and construct validity in measuring CT disposition. Their developmental model highlighted that decomposition and abstraction are key predictors of AT, evaluation, and generalization, suggesting their critical role in CT development.
So, there is a lack of CFA-specialized studies on AT published in the last five years, independent of CT, focused solely on problem solving, and on university/college undergraduate students (young adults).
Rubric
for algorithmic thinking
According to Bubica and Boljat (2021), algorithmic solutions are always difficult to evaluate because “in the process of creating a model of evidence, it is crucial to explore all possible evidence of a pupil’s knowledge without losing sight of the different ways in which it could be expressed within the context and the requirements of the task itself” (p. 442). Therefore, one way to assess students’ performance objectively and methodically is through a rubric (Chowdhury, 2019).
Furthermore, it is highly recommended to construct rubrics to assess students’ learning, cognitive development, or skills, based on Bloom’s taxonomy of educational objectives (Moreira Gois et al., 2023; Noor et al., 2023). This taxonomy of educational objectives includes Knowledge (knowing), understanding, application, analysis, synthesis, and evaluation (Bloom & Krathwohl, 1956).
Although some more or less precise recent operational definitions have been proposed for AT (Juškevičienė & Dagienė, 2018; Lafuente Martínez et al., 2022; Park & Jun, 2023), these do not include a specific (or general) rubric to assess performance levels for each of the components or factors these operational definitions claim to compose the AT construct.
The only rubric to measure AT development found, independent of CT, based on open-ended problem solving for undergraduate students, is that by Navas-López’s (2021) master thesis. This study has a correlational scope and does not include construct validation for the rubric.
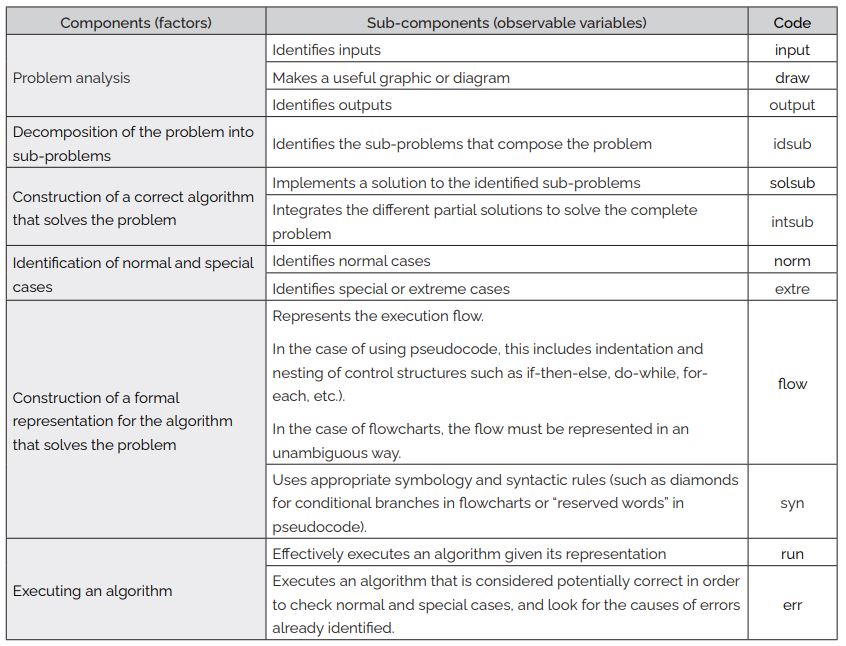
Navas-López (2021) proposed two operationalizations for AT: One operationalization is for a beginner’s AT level, and the other is for an expert’s AT level. In the skills list that composes a beginner’s AT, the educational objectives of Knowledge (knowing), understanding and application (execution) of algorithms have been included. Table 1 shows the latent variables (components or factors) and observable variables of the operationalization for a beginner’s AT, according to this proposal, and Figure 1 shows the corresponding structural model.
Table
1
Generic
operationalization of a beginner’s algorithmic thinking

Note. Translation of Table 3.3 from Navas-López (2021, p. 60)
Figure
1
Structural
model of a beginner’s algorithmic thinking operationalization
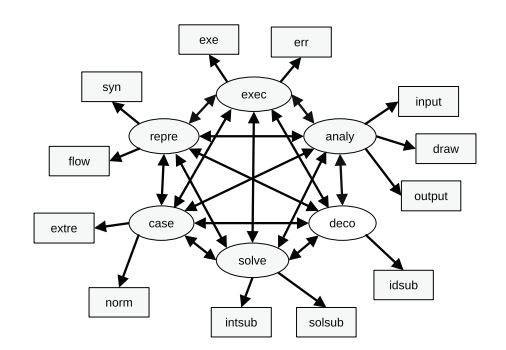
Note. Own elaboration from factors and observable variables from Table 1.
Navas-López
(2021) explains that he primarily used the definition provided by
Futschek (2006) due to its wide referencing in multiple publications
on AT and CT. However, he supplemented his operational definition
with the definition by Grozdev and Terzieva (2015), particularly
concerning problem decomposition, the relationship between
sub-problems, and the formalization of algorithm representation.
Finally, the notion of algorithm debugging from Sadykova and Usolzev
(2018) was incorporated.
This proposal also incorporates the components outlined by Stephens and Kadijevich (2020): Abstraction in problem analysis and identification of sub-problems, decomposition explicitly, and algorithmization, as understood by Lehmann (2023).
Navas-López (2021) also developed a generic analytic rubric to assess a beginner’s AT level from its factors for a given problem, following the steps of Mertler’s (2001) scoring rubric design and the template presented by Cebrián de la Serna and Monedero Moya (2014). Table 2 shows the detailed rubric.
Table
2
Generic
analytic rubric to assess a beginner’s algorithmic thinking level
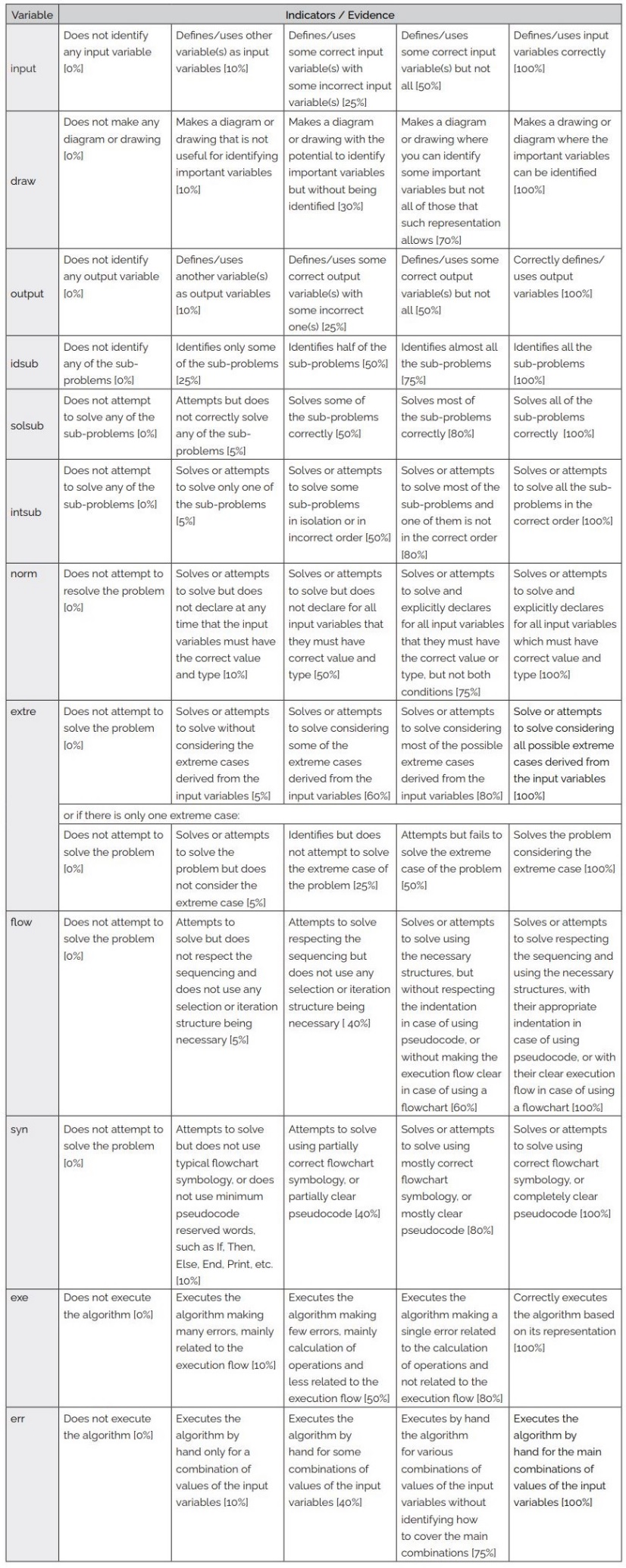
Note. Translation of Table 3.4 from Navas-López (2021, pp. 61-65)
Navas-López (2021) also developed two specific rubrics for the two problems, the solution of which is an algorithm contained in the instrument used (p2 and p4). These two rubrics are versions derived from the one presented in Table 2 but adjusted to the particularities of both problems. Besides, both problems do not include the execution of the resulting algorithm due to time restrictions during the administration of the instrument, so they do not consider the component "Executing an algorithm" (from Table 1), that is, the exe and err variables. One of the problems did not require a graphic or diagram to be analyzed and solved, so it does not include the draw variable. So, observable variables assessed for problem p2 are: p2. input, p2.output, p2.idsub, p2.solsub, p2.intsub, p2.norm, p2.extre, p2.flow, p2.syn; and for problem p4 are: p4.input, p4.draw, p4.output, p4.idsub, p4.solsub, p4.intsub, p4.norm, p4.extre, p4.flow, p4.syn.
This research aims to construct validation for the specific rubrics applied by Navas-López (2021) as part of his operational definition for assessing AT in undergraduate students. Specifically, this construct validation will be carried out through CFA applied to several models proposed by the researcher based on the grouping of the measured variables for the two problems in the original measurement instrument.
Method
Problems p2 and p4, extracted from the instrument developed by Navas-López (2021), were administered to a sample of 88 undergraduate students enrolled in three academic programs offered by the School of Mathematics at the University of El Salvador. The participants, aged 17 to 33 (M: 20.88 years, SD: 2.509 years), included 41 women (46.59%), 46 men (52.27%), and 1 participant who did not report their gender. The overall grades of the subjects ranged from 6.70 to 9.43 on a scale of 0.00 to 10.00 (M: 7.64, SD: 0.57). The total student population at the time of data collection was 256, and a convenience sampling approach was employed during regular face-to-face class sessions across different academic years (first year, second year, and third year). The researcher verbally communicated the instructions for solving the problems, after which students individually solved them on paper, with the option to ask questions for clarification.
The translation of Navas-López’s (2021) problem p2 is:
A school serving students from seventh to ninth grade organizes a trip every two months, including visits to a museum and a theater performance. The school principal has established a rule that one responsible adult must accompany every 15 students for each trip. Additionally, it is mandated that each trip be organized by a different teacher, with rotating responsibilities. Consequently, each teacher may go several months (or even years) without organizing a trip, and when it is their turn again, they may not remember the steps to follow. Develop a simple algorithm that allows any organizer reading it to calculate the cost of the trip (to determine how much each student should contribute). (p. 70)
The translation of Navas-López’s (2021) problem p4 is:
As you know, most buses entering our country for use in public transportation have their original seats removed and replaced with others that have less space between them to increase capacity and reduce comfort.
The company 'Tight Fit Inc.' specializes in providing this modification service to public transportation companies when they 'bring in a new bus' (which we already know is not only used but also discarded in other countries).
Write an algorithm for the operational manager (the head of the workers) to perform the task of calculating how many seats should be installed and the distance between them. Assume that the original seats have already been removed, and the 'new' ones are in a nearby warehouse, already assembled and ready to be installed. Since the company is dedicated to this, it has an almost unlimited supply of 'new' seats. (p. 71)
To assess the students’ procedures, the researcher employed the dedicated rubrics for these problems outlined by Navas-López (2021, pp. 77-98). Scores on a scale from 0 to 100 were assigned to the variables: p2.input, p2.output, p2.idsub, p2.solsub, p2.intsub, p2.norm, p2.extre, p2.flow, p2.syn, p4.input, p4.draw, p4.output, p4.idsub, p4.solsub, p4.intsub, p4.norm, p4.extre, p4.flow, p4.syn.
These 19 observable variables have been grouped in four different ways to construct the models for evaluation. The first group of models includes all 19 variables separately (p2&p4). The second group of models includes only the variables related to the first problem (p2). The third group of models includes only the variables related to the second problem (p4). Finally, the fourth group of models comprises intermediate variables obtained from the average of the corresponding variables in both problems (p2+p4), as follows:
input:= (p2.input + p4.input)/2
draw:= p4.draw
output:= (p2.output + p4.output)/2
idsub:= (p2.idsub + p4.idsub)/2
solsub:= (p2.solsub + p4.solsub)/2
intsub:= (p2.intsub + p4.intsub)/2
norm:= (p2.norm + p4.norm)/2
extre:= (p2.extre + p4.extre)/2
flow:= (p2.flow + p4.flow)/2
syn:= (p2.syn + p4.syn)/2
To assess the feasibility of conducting factor analysis on these four ways of grouping the observable variables, the researcher performs a data adequacy analysis. For assessing reliability, the Cronbach’s alpha coefficient was utilized, and to evaluate construct validity, a CFA was applied to the models described in Table 3. All calculations were carried out using R language, version 4.3.2.
Table
3
Conformation
of the evaluated factorial models
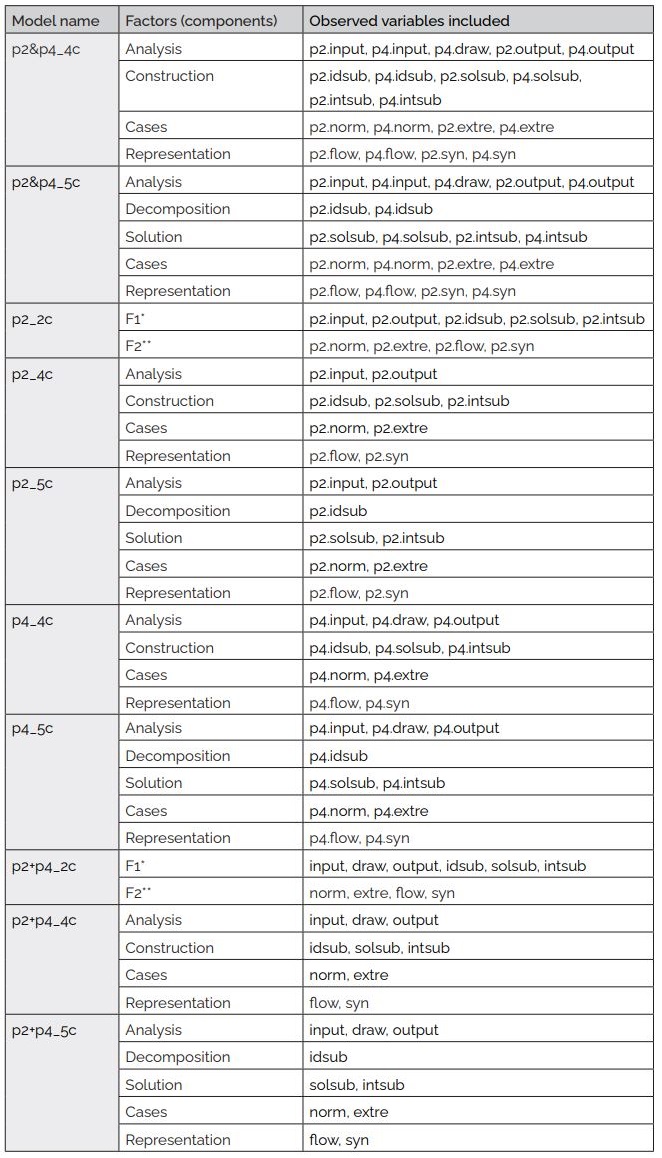
Note. *General solution, **Particular cases and representation.
To
evaluate the different models, the absolute fit indices chi-square
(![]() ),
relative chi-square (
),
relative chi-square (![]() ),
RMSEA, SRMR, and the incremental fit indices TLI, CFI, NFI, and GFI
were used. The evaluation was based on the respective cut-off values
recommended by Jordan Muiños (2021) and Moss (2016), as presented in
Table 4.
),
RMSEA, SRMR, and the incremental fit indices TLI, CFI, NFI, and GFI
were used. The evaluation was based on the respective cut-off values
recommended by Jordan Muiños (2021) and Moss (2016), as presented in
Table 4.
Table
4
Indices’
cut-off values for Confirmatory Factor Analysis

Note. Own elaboration based on criteria from Jordan Muiños (2021) and Moss (2016).
Results
Of the 88 students, 82 attempted to solve problem p2 (6 did not attempt), 76 attempted to solve problem p4 (12 did not attempt), and 70 attempted to solve both problems. Everyone attempts to solve at least one problem. Cronbach’s Alpha for problem p2 was 0.84, for problem p4 was 0.85, and for both problems (all data) was 0.88. Anderson-Darling test was applied to determine normality, and results showed no one observed variable are normal.
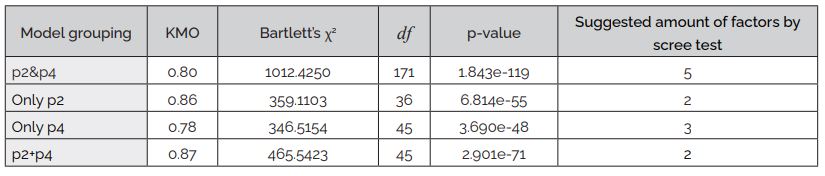
Kaiser-Meyer-Olkin measure was computed to assess the adequacy of the data for conducting a factor analysis. Additionally, Bartlett's test of sphericity was employed to determine whether there was sufficient correlation among the variables to proceed with a factor analysis. The scree test was also utilized to calculate the minimum number of recommended factors. This test defined the two-component models. The results presented in Table 5 reveal that there was a significant relationship among observable variables within four model groupings, supporting the feasibility of conducting a CFA.
Table
5
Results
of data adequacy analysis for studied model groupings
For
CFA, the WLSMV estimator (weighted least squares with robust standard
errors and mean- and variance-adjusted test statistics) was used,
following Brown's (2006) recommendations for ordinal, non-normal
observable variables.
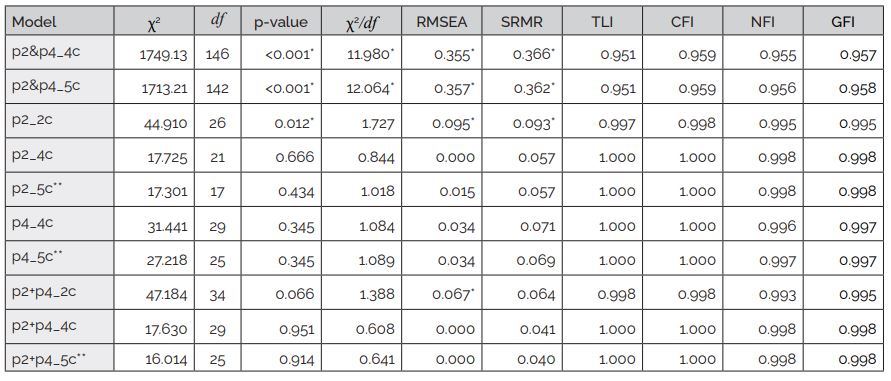
Corresponding indices were calculated for all models. Table 6 displays the calculated indices. All models achieve good values for incremental fit indices. However, models p2&p4_4c and p2&p4_5c fail in all absolute fit indices. Models p2_2c and p2+p4_2c do not successfully meet all absolute fit indices. For models p2_5c, p4_5c, and p2+p4_5c, all directly based on operationalization in Table 1, it was impossible to compute standard errors in CFA. Since standard errors represent how closely the model's parameter estimates approximate the true population parameters (Brown, 2006), all models with 5 components (factors) must be discarded.
Table
6
Results
from the CFA conducted
Note.
*Does not meet according to cut-off values in Table 4.
**Could
not compute standard errors.
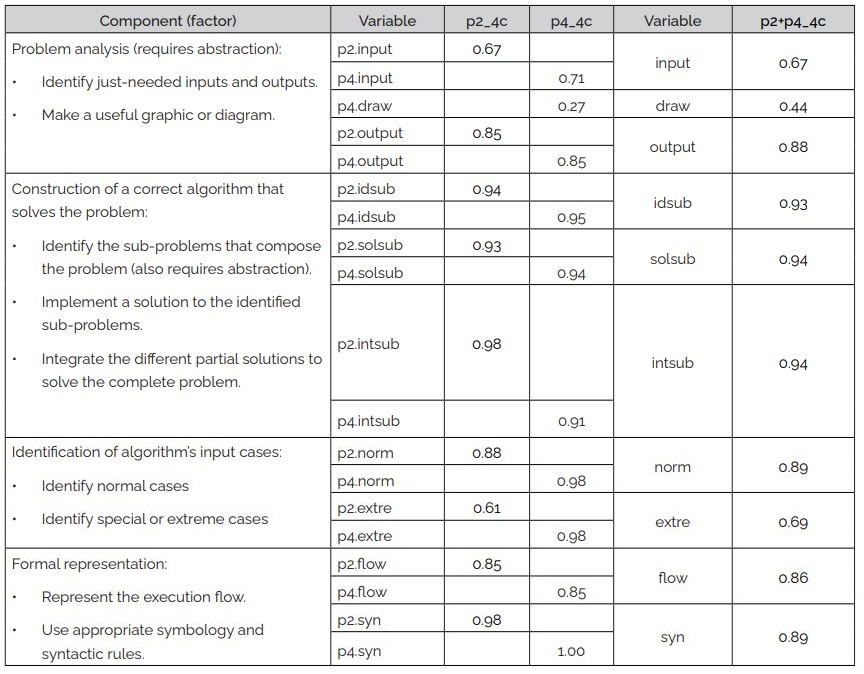
Only
last three models with 4 components (factors) has very good
psychometric properties. They are very similar to operationalization
in Table 1, but in these models, decomposition-related observed
variables (p2.idsub and p4.idsub) are placed together with
algorithm-construction-related variables (p2.solsub, p2.intsub,
p4.solsub and p4.intsub) inside the same factor. The factor loadings
of these three models are shown in Table 7.
Table
7
Factor
loadings of observed variables in viable four-component models
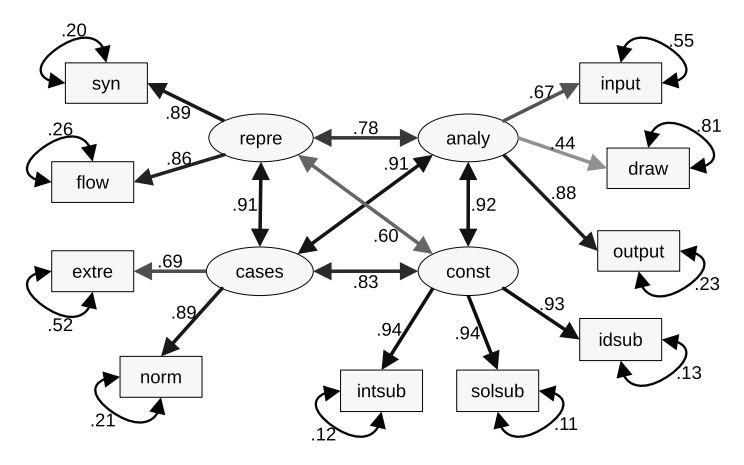
Figure
2 displays the structural equation modelling (SEM) diagram for the
p2+p4_4c model, depicting factor loadings, residuals, and covariances
between factors. Notably, only one-factor loading is relatively weak
and pertains to the variable "draw." Conversely, all other
factor loadings exhibit reasonably high values.
Figure
2
SEM
diagram for validated model p2+p4_4c with four components for AT
Discussion
and conclusion
Grading consistency can be challenging, but rubrics serve as a standard scoring tool to reduce inconsistencies and assess students' work more efficiently and transparently (Chowdhury, 2019). Rubrics are crucial for evaluating complex cognitive skills like AT. Although analytic rubrics can slow down the scoring process because they require examining multiple skills individually (Mertler, 2001), their detailed analysis is valuable for understanding and developing AT (Lehmann, 2023).
Constructing reliable open-ended problems to assess AT is challenging due to the relation between problem complexity and students’ prior experience. Thus, several considerations are essential: using a standard complexity metric for algorithms (Kayam et al., 2016), employing a general rubric for assessing CT activities (Otero Avila et al., 2019), and adapting problem complexity to students' levels (Bubica & Boljat, 2021).
The lack of consensus on the differences between CT and AT hinders the development of a standard rubric for AT. For instance, Bubica and Boljat’s (2021) and Ortega Ruipérez and Asensio Brouard’s (2021) interpretations of CT align with Stephens and Kadijevich’s (2020) interpretation of AT. These diverse interpretations complicate the validation of their operational definitions.
Despite these difficulties, the design, construction, and construct validation of an assessment rubric for AT represent a valuable effort. Evaluating CT (Poulakis & Politis, 2021) and AT (Stephens & Kadijevich, 2020) remains an urgent concern for educational researchers. Therefore, any endeavor to advance towards a comprehensive operational definition of AT with both content and construct validity must be greatly appreciated.
In this study, the CFA conducted on undergraduate students (aged 17-33) led to an operational definition for AT composed of four components: Problem analysis, algorithm construction, input cases identification, and algorithm representation (as shown in Table 7). This result is confirmed by the good psychometric properties of the three four-factor models, with the two problems considered separately, p2_4c and p4_4c, and with the averaged results from both problems, p2+p4_4c (see Table 6).
These results provide more detail than the two-factor model (problem representation and problem-solving) by Ortega Ruipérez and Asensio Brouard (2021) for adolescents and the unifactorial model by Lafuente Martínez et al. (2022) for adults. However, comparability with Bubica and Boljat (2021) and Sung (2022) is limited, as both focus on children, and their models' factor loadings and psychometric properties are unsatisfactory. This may be due to children's ongoing cognitive development, as Sung (2022) notes. Indeed, higher-order thinking skills, such as complex problem-solving, develop as children transition to adolescence (Greiff et al., 2015).
However, there are significant limitations to consider. The sample size of 88 subjects is relatively small, potentially limiting the generalizability of the results. Moreover, the use of convenience sampling introduces bias, making it unclear if the sample represents all undergraduate students. These limitations underscore the need for cautious interpretation and highlight the necessity for future studies with larger, more diverse samples to validate these findings.
Furthermore, Navas-López's (2021) operational definition for AT lacks complete construct validation, particularly regarding the "running" component (see Table 1). Future research should address this by employing larger samples and using a comprehensive instrument (including a broader rubric) that evaluates a range of problems, akin to p2 and p4, for grading the initial 10 variables, alongside proposed algorithms for the run and err variables (see Table 2).
In conclusion, while this study advances toward a detailed operational definition of AT, the sample size and sampling method constraints must be acknowledged. Continued research is crucial to strengthen the reliability and applicability of these findings, thereby facilitating the development of robust assessment tools for AT.
Notes:
Final
approval of the article:
Verónica
Zorrilla de San Martín, PhD, Editor in Charge of the journal.
Authorship
contribution:
Eduardo
Adam Navas-López: conceptualization, data curation, formal analysis,
research, methodology, software, validation, visualization, writing
of the draft and review of the manuscript.
Availability
of data:
The
dataset supporting the findings of this study is not publicly
available. The research data will be made available to reviewers upon
request.
References
Bacelo, A., & Gómez-Chacón, I. M. (2023). Characterizing algorithmic thinking: A university study of unplugged activities. Thinking Skills and Creativity, 48, Article 101284. https://doi.org/10.1016/j.tsc.2023.101284
Bloom, B. S., & Krathwohl, D. R. (1956). Taxonomy of educational objectives: Cognitive domain (Vol. 1). McKay.
Brown, T. A. (2006). Confirmatory factor analysis for applied research. Guilford Press.
Bubica, N., & Boljat, I. (2021). Assessment of Computational Thinking – A Croatian Evidence-Centered Design Model. Informatics in Education, 21(3), 425-463. https://doi.org/10.15388/infedu.2022.17
Cebrián de la Serna, M., & Monedero Moya, J. J. (2014). Evolución en el diseño y funcionalidad de las rúbricas: Desde las rúbricas «cuadradas» a las erúbricas federadas. REDU. Revista de Docencia Universitaria, 12(1), 81-98. https://doi.org/10.4995/redu.2014.6408
Chen, P., Yang, D., Metwally, A. H. S., Lavonen, J., & Wang, X. (2023). Fostering computational thinking through unplugged activities: A systematic literature review and meta-analysis. International Journal of STEM Education, 10(1), Article 47. https://doi.org/10.1186/s40594-023-00434-7
Chowdhury, F. (2019). Application of Rubrics in the Classroom: A Vital Tool for Improvement in Assessment, Feedback and Learning International Education Studies, 12(1), 61–68. International Education Studies, 12(1), 61–68. https://doi.org/10.5539/ies.v12n1p61
Futschek, G. (2006). Algorithmic Thinking: The Key for Understanding Computer Science. In R. T. Mittermeir (Ed.), International conference on informatics in secondary schools—Evolution and perspectives (pp. 159–168). Springer-Verlag.
Greiff, S., Wüstenberg, S., Goetz, T., Vainikainen, M.-P., Hautamäki, J., & Bornstein, M. H. (2015). A longitudinal study of higher-order thinking skills: Working memory and fluid reasoning in childhood enhance complex problem-solving in adolescence. Frontiers in Psychology, 6, Article 1060. https://doi.org/10.3389/fpsyg.2015.01060
Grover, S. (2017). Assessing algorithmic and computational thinking in K-12: Lessons from a middle school classroom. In P. J. Rich & C. B. Hodges (Eds.), Emerging research, practice, and policy on computational thinking (pp. 269–288). Springer. https://doi.org/10.1007/978-3-319-52691-1_17
Grover, S., & Pea, R. (2018). Computational thinking: A competency whose time has come. In S. Sentance, E. Barendsen, & C. Schulte (Eds.), Computer science education: Perspectives on teaching and learning in school. Bloomsbury Publishing.
Grozdev, S., & Terzieva, T. (2015). A didactic model for developmental training in computer science. Journal of Modern Education Review, 5(5), 470-480. https://doi.org/10.15341/jmer(2155-7993)/05.05.2015/005
Jordan Muiños, F. M. (2021). Cut-off value of the fit indices in Confirmatory Factor Analysis. {PSOCIAL}, 7(1), 66-71. https://publicaciones.sociales.uba.ar/index.php/psicologiasocial/article/view/6764
Juškevičienė, A. (2020). Developing Algorithmic Thinking Through Computational Making. In D. Gintautas, B. Jolita, & K. Janusz (Eds.), Data Science: New Issues, Challenges and Applications (Vol. 869, pp. 183-197). Springer. https://doi.org/10.1007/978-3-030-39250-5_10
Juškevičienė, A., & Dagienė, V. (2018). Computational Thinking Relationship with Digital Competence. Informatics in Education, 17(2), 265-284. https://doi.org/10.15388/infedu.2018.14
Kadijevich, D. M., Stephens, M., & Rafiepour, A. (2023). Emergence of Computational/Algorithmic Thinking and Its Impact on the Mathematics Curriculum. In Y. Shimizu & R. Vithal (Eds.), Mathematics Curriculum Reforms Around the World (pp. 375-388). Springer International Publishing. https://doi.org/10.1007/978-3-031-13548-4_23
Kanaki, K., & Kalogiannakis, M. (2022). Assessing Algorithmic Thinking Skills in Relation to Age in Early Childhood STEM Education. Education Sciences, 12(6), Article 380. https://doi.org/10.3390/educsci12060380
Kayam, M., Fuwa, M., Kunimune, H., Hashimoto, M., & Asano, David. K. (2016). Assessing your algorithm: A program complexity metrics for basic algorithmic thinking education. In 11th International Conference on Computer Science & Education (ICCSE), 309–313. https://doi.org/10.1109/ICCSE.2016.7581599
Kirçali, A. Ç., & Özdener, N. (2023). A Comparison of Plugged and Unplugged Tools in Teaching Algorithms at the K-12 Level for Computational Thinking Skills. Technology, Knowledge and Learning, 28(4), 1485-1513. https://doi.org/10.1007/s10758-021-09585-4
Knuth, D. E. (1974). Computer Science and its Relation to Mathematics. The American Mathematical Monthly, 81(4), 323–343. https://doi.org/10.1080/00029890.1974.11993556
Korkmaz, Ö., Çakir, R., & Özden, M. Y. (2017). A validity and reliability study of the computational thinking scales (CTS). Computers in Human Behavior, 72, 558-569. https://doi.org/10.1016/j.chb.2017.01.005
Lafuente Martínez, M., Lévêque, O., Benítez, I., Hardebolle, C., & Zufferey, J. D. (2022). Assessing Computational Thinking: Development and Validation of the Algorithmic Thinking Test for Adults. Journal of Educational Computing Research, 60(6), 1436-1463. https://doi.org/10.1177/07356331211057819
Lehmann, T. H. (2023). How current perspectives on algorithmic thinking can be applied to students’ engagement in algorithmatizing tasks. Mathematics Education Research Journal. https://doi.org/10.1007/s13394-023-00462-0
Lockwood, E., DeJarnette, A. F., Asay, A., & Thomas, M. (2016). Algorithmic Thinking: An Initial Characterization of Computational Thinking in Mathematics. In M. B. Wood, E. E. Turner, M. Civil, & J. A. Eli (Eds.), Proceedings of the 38th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PMENA 38) (pp. 1588–1595). ERIC. https://eric.ed.gov/?id=ED583797
Martins-Pacheco, L. H., da Cruz Alves, N., & von Wangenheim, C. G. (2020). Educational Practices in Computational Thinking: Assessment, Pedagogical Aspects, Limits, and Possibilities: A Systematic Mapping Study. In H. C. Lane, S. Zvacek, & J. Uhomoibhi (Eds.), Computer Supported Education (pp. 442-466). Springer International Publishing. https://doi.org/10.1007/978-3-030-58459-7_21
Mertler, C. A. (2001). Designing scoring rubrics for your classroom. Practical assessment, research, and evaluation, 7(1), Article 25. https://doi.org/10.7275/gcy8-0w24
Moreira Gois, M., Eliseo, M. A., Mascarenhas, R., Carlos Alcântara De Oliveira, I., & Silva Lopes, F. (2023). Evaluation rubric based on Bloom's taxonomy for assessment of students learning through educational resources. In 15th International Conference on Education and New Learning Technologies, (pp. 7765-7774). https://doi.org/10.21125/edulearn.2023.2021
Moss, S. (2016, June 27). Fit indices for structural equation modelling. Sicotest.com. https://www.sicotests.com/newpsyarticle/Fit-indices-for-structural-equation-modeling
Navas-López, E. A. (2021). Una Caracterización del Desarrollo del Pensamiento Algorítmico de los Estudiantes de las carreras de Licenciatura en Matemática y Licenciatura en Estadística de la sede central de la Universidad de El Salvador en el período 2018-2020 [Master’s Thesis, Universidad de El Salvador]. https://hdl.handle.net/20.500.14492/12041
Navas-López, E. A. (2024). Relaciones entre la matemática, el pensamiento algorítmico y el pensamiento computacional. IE Revista de Investigación Educativa de la REDIECH, 15, e1929. https://doi.org/10.33010/ie_rie_rediech.v15i0.1929
Noor, N. M. M., Mamat, N. F. A., Mohemad, R., & Mat, N. A. C. (2023). Systematic Review of Rubric Ontology in Higher Education. International Journal of Advanced Computer Science and Applications, 14(10), 147-155. https://doi.org/10.14569/IJACSA.2023.0141016
Nordby, S. K., Bjerke, A. H., & Mifsud, L. (2022). Computational Thinking in the Primary Mathematics Classroom: A Systematic Review. Digital Experiences in Mathematics Education, 8(1), 27-49. https://doi.org/10.1007/s40751-022-00102-5
Oomori, Y., Tsukamoto, H., Nagumo, H., Takemura, Y., Iida, K., Monden, A., & Matsumoto, K. (2019). Algorithmic Expressions for Assessing Algorithmic Thinking Ability of Elementary School Children. In 2019 IEEE Frontiers in Education Conference (FIE), 1-8. https://doi.org/10.1109/FIE43999.2019.9028486
Ortega Ruipérez, B., & Asensio Brouard, M. (2021). Evaluar el Pensamiento Computacional mediante Resolución de Problemas: Validación de un Instrumento de Evaluación. Revista Iberoamericana de Evaluación Educativa, 14(1), 153-171. https://doi.org/10.15366/riee2021.14.1.009
Otero Avila, C., Foss, L., Bordini, A., Simone Debacco, M., & da Costa Cavalheiro, S. A. (2019). Evaluation Rubric for Computational Thinking Concepts. In IEEE 19th International Conference on Advanced Learning Technologies (ICALT), 279-281. https://doi.org/10.1109/ICALT.2019.00089
Park, H., & Jun, W. (2023). A Study of Development of Algorithm Thinking Evaluation Standards. International Journal of Applied Engineering and Technology, 5(2), 53-58.
Poulakis, E., & Politis, P. (2021). Computational Thinking Assessment: Literature Review. In T. Tsiatsos, S. Demetriadis, A. Mikropoulos, & V. Dagdilelis (Eds.), Research on E-Learning and ICT in Education (pp. 111-128). Springer International Publishing. https://doi.org/10.1007/978-3-030-64363-8_7
Román-González, M., Moreno-León, J., & Robles, G. (2019). Combining Assessment Tools for a Comprehensive Evaluation of Computational Thinking Interventions. In S. C. Kong & H. Abelson (Eds.), Computational Thinking Education (pp. 79-98). Springer. https://doi.org/10.1007/978-981-13-6528-7_6
Sadykova, O. V., & Usolzev, A. (2018). On the concept of algorithmic thinking. In SHS Web Conferences – International Conference on Advanced Studies in Social Sciences and Humanities in the Post-Soviet Era (ICPSE 2018), 55. https://doi.org/10.1051/shsconf/20185503016
Selby, C. C., & Woollard, J. (2013). Computational Thinking: The Developing Definition. In 18th annual conference on innovation and technology in computer science education. https://eprints.soton.ac.uk/356481/
Shute, V. J., Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review, 22, 142–158. https://doi.org/10.1016/j.edurev.2017.09.003
Stephens, M., & Kadijevich, D. M. (2020). Computational/Algorithmic Thinking. In S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 117-123). Springer International Publishing. https://doi.org/10.1007/978-3-030-15789-0_100044
Sung, J. (2022). Assessing young Korean children’s computational thinking: A validation study of two measurements. Education and Information Technologies, 27(9), 12969–12997. https://doi.org/10.1007/s10639-022-11137-x
Tang, X., Yin, Y., Lin, Q., Hadad, R., & Zhai, X. (2020). Assessing computational thinking: A systematic review of empirical studies. Computers & Education, 148, 1-22. https://doi.org/10.1016/j.compedu.2019.103798
Tsai, M. J., Liang, J. C., Lee, S. W. Y., & Hsu, C. Y. (2022). Structural Validation for the Developmental Model of Computational Thinking. Journal of Educational Computing Research, 60(1), 56-73. https://doi.org/10.1177/07356331211017794
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining Computational Thinking for Mathematics and Science Classrooms. Journal of Science Education and Technology, 25(1), 127-147. https://doi.org/10.1007/s10956-015-9581-5
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35. https://doi.org/10.1145/1118178.1118215
Wing, J. M. (2017). Computational thinking’s influence on research and education for all. Italian Journal of Educational Technology, 25(2), 7–14. https://doi.org/10.17471/2499-4324/922
Zúñiga Muñoz, R. F., Hurtado Alegría, J. A., & Robles, G. (2023). Assessment of Computational Thinking Skills: A Systematic Review of the Literature. IEEE Revista Iberoamericana de Tecnologias del Aprendizaje, 18(4), 319-330. https://doi.org/10.1109/RITA.2023.3323762